.Introduction
This work investigates a new learning formulation called dynamic group sparsity. It is a natural extension of the standard sparsity concept in compressive sensing, and is motivated by the observation that in some practical sparse data the nonzero coefficients are often not random but tend to be clustered. Intuitively, better results can be achieved in these cases by reasonably utilizing both clustering and sparsity priors. Motivated by this idea, we have developed a new greedy sparse recovery algorithm, which prunes data residues in the iterative process according to both sparsity and group clustering priors rather than only sparsity as in previous methods. The proposed algorithm can recover stably sparse data with clustering trends using far fewer measurements and computations than current state-of-the-art algorithms with provable guarantees. Moreover, our algorithm can adaptively learn the dynamic group structure and the sparsity number if they are not available in the practical applications. DGS can be used in the applications on Compressive Sensing, Video Background Subtraction and Visual Tracking and so on.
Applications:
2) Video Background Subtraction
Reference
Junzhou Huang, Xiaolei Huang, Dimitris Metaxas, ”Learning with Dynamic Group Sparsity”, The 12th International Conference on Computer Vision, Kyoto, Japan, October 2009. [SLIDES] [CODE]
Baiyang Liu, Lin Yang, Junzhou Huang, Peter Meer, Leiguang Gong, Casimir Kulikowski, ”Robust and Fast Collaborative Tracking with Two StageSparse Optimization”, The 11th European Conference on Computer Vision, Crete, Greece, September, 2010.
Notice: The codes was tested on Windows and MATLAB 2008. If you have any suggestions or you have found a bug, please contact us via email at jzhuang@uta.edu
DGS Examples
 |
Figure 1.1 An example of
dynamic group sparse data: (a) one video frame, (b) the foreground
image, (c) the foreground mask and (d) the background subtracted
image with the proposed algorithm. |
| Problem Formulation | |
| |
|
|
|
DGS Algorithms
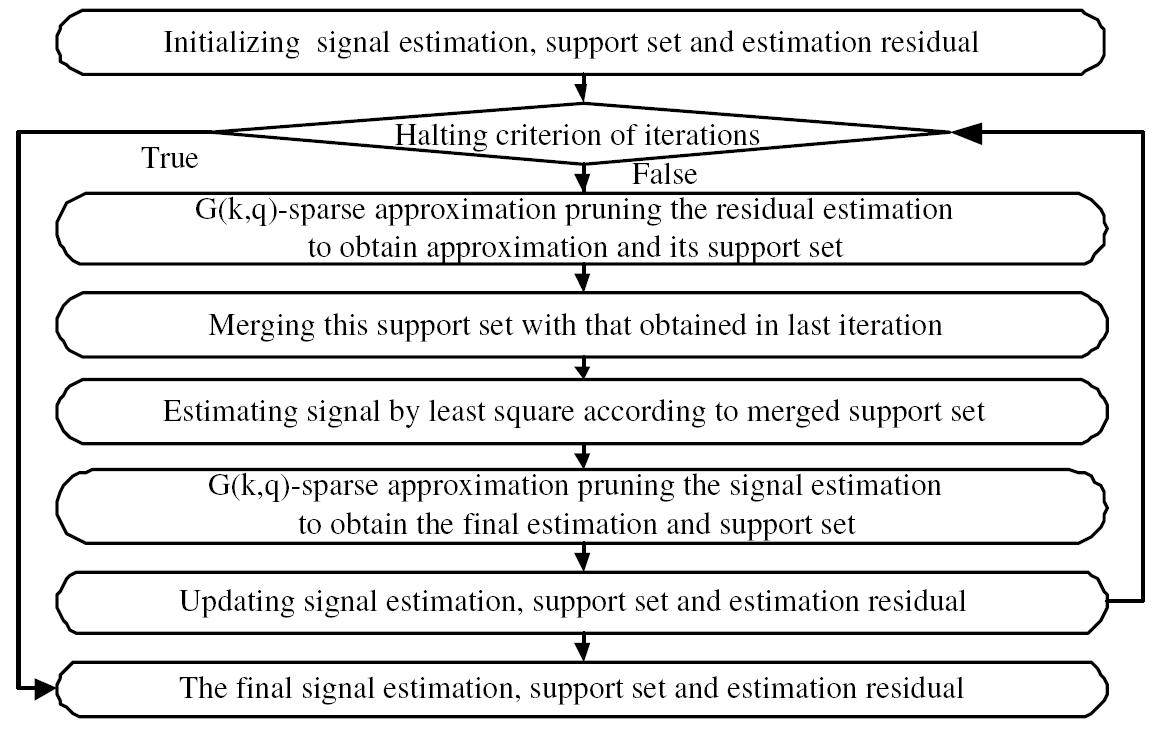 |
| Figure 1.2 Main steps of the proposed
algorithm |
Related Sources
Group Lasso and Multiple Kernel Learning
Matlab Implementaion for Group Lasso