Junzhou Huang

Transformation Invariance Sparse Representation

.Introduction

Sparse representation in compressive sensing is gaining increasing attention due to its success in various applications. As we demonstrate in this paper, however, image sparse representation is sensitive to image plane transformations such that existing approaches can not reconstruct the sparse representation of a geometrically transformed image. We introduce a simple technique for obtaining transformation-invariant image sparse representation. It is rooted in two observations: 1) if the aligned model images of an object span a linear subspace, their transformed versions with respect to some group of transformations can still span a linear subspace in a higher dimension; 2) if a target (or test) image, aligned with the model images, lives in the above subspace, its pre-alignment versions would get closer to the subspace after applying estimated transformations with more and more accurate parameters. These observations motivate us to project a potentially unaligned target image to random projection manifolds defined by the model images and the transformation model. Each projection is then separated into the aligned projection target and a residue due to misalignment. The desired aligned projection target is then iteratively optimized by gradually diminishing the residue. In this framework, we can simultaneously recover the sparse representation of a target image and the image plane transformation between the target and the model images. We have applied the proposed methodology to two applications: face recognition, and dynamic texture registration. The improved performance over previous methods that we obtain demonstrates the effectiveness of the proposed approach.

[Romanian Version] Kindly translated by Maxim Petrenko

.Download

Junzhou Huang, Xiaolei Huang, Dimitris Metaxas, ”Simultaneous Image Transformation and Sparse Representation Recovery”, IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Anchorage, Alaska, USA, 2008. [PDF] [POSTER] [CODE]

Notice: The codes was tested on Windows and MATLAB 2008. If you have any suggestions or you have found a bug, please contact us via email at jzhuang@uta.edu.

Gradient Projection for Sparse Reconstruction

Visual Comparison

Figure. Sparse representation results given unaligned test images. Training images (a), test images (b), results by Randomfaces (c), results by the proposed approach (d).

Recognition Comparisons

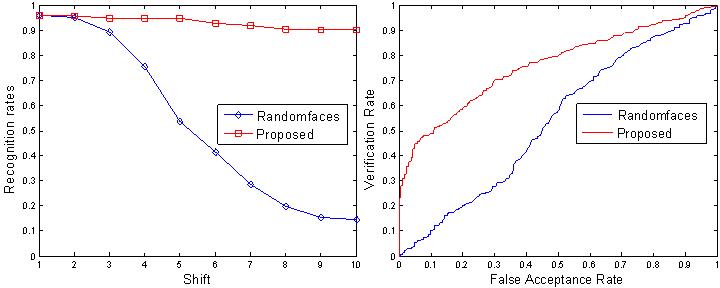Figure. Identification results and ROC curves. Left is for Identification and right is for verification