.Introduction
We consider the minimization of a smooth convex function regularized by the composite prior models. This problem is generally difficult to solve even each subproblem regularized by one prior model is convex and easy. In this paper, we present two algorithms to effectively solve it. First, the original problem is decomposed into multiple simpler subproblems. Then, these subproblems are efficiently solved by existing techniques in parallel. Finally, the result of the original problem is obtained from the weighted average of solutions of subproblems in an iterative framework. The proposed composite splitting algorithms are applied to the compressed MR image reconstruction and low-rank tensor completion respectively. Numerous experiments demonstrate the superior performance of the proposed algorithm in terms of both the accuracy and computation complexity.
.Download
Junzhou Huang, Shaoting Zhang and Dimitris Metaxas. "Fast Optimization for Mixture Prior Models", In Proc. of the 11th European Conference on Computer Vision, ECCV'2010. [PDF] [CODE]
Junzhou Huang, Shaoting Zhang, Hongsheng Li, Dimitris Metaxas, "Composite Splitting Algorithms for Convex Optimization", Computer Vision and Image Understanding, Volume 115, Number 12, pp. 1610-1622, December 2011.[PDF] [CODE]
Junzhou Huang, Shaoting Zhang, Dimitris Metaxas, "Efficient MR Image Reconstruction for Compressed MR Imaging", Medical Image Analysis, Volume 15, Issue 5, pp. 670-679, October 2011. [CODE]
Notice: The codes was tested on Windows and MATLAB 2008. If you have any suggestions or you have found a bug, please contact us via email at jzhuang@uta.edu
Efficient Image Reconstruction in Compressive Sensing MRI
Visual Comparison
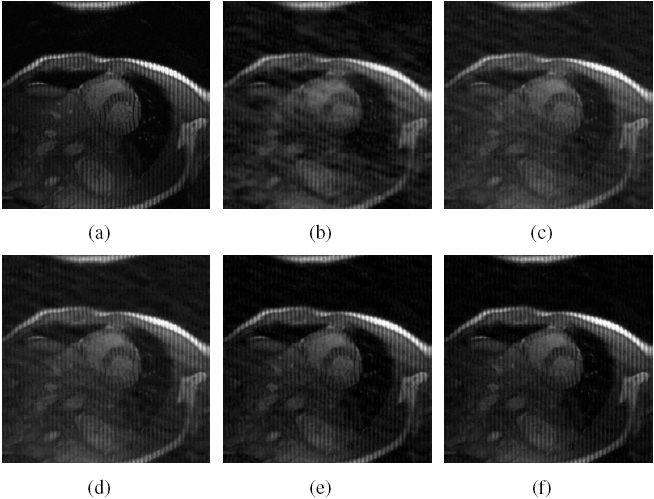 |
Figure.
Cardiac MR image reconstruction from
20% sampling (a) Original image; (b), (c), (d) (e) and (f)
are the reconstructed images by the CG [1], TVCMRI [2], RecPF
[3], CSA and FCSA. Their SNR are 9.86, 14.43, 15.20, 16.46
and 17.57 (db). Their CPU time are 2.87, 3.14, 3.07, 2.22
and 2.29 (s). |
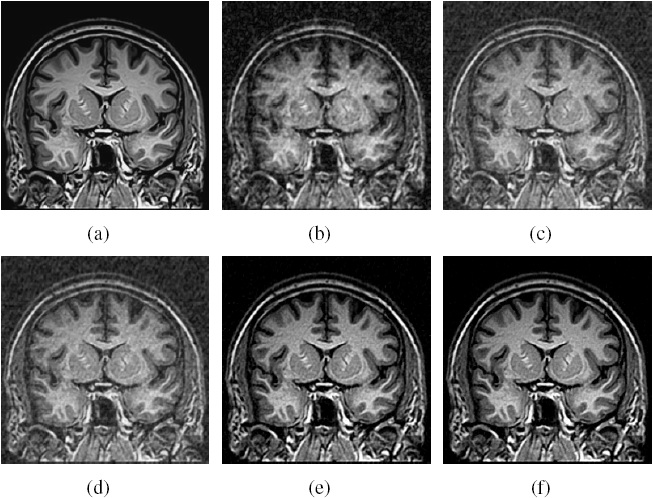 |
Figure.
Brain MR image reconstruction from 20%
sampling (a) Original image; (b), (c), (d) (e) and (f) are
the reconstructed images by the CG [1], TVCMRI [2], RecPF
[3], CSA and FCSA. Their SNR are 8.71, 12.12, 12.40, 18.68
and 20.35 (db). Their CPU time are 2.75, 3.03, 3.00, 2.22
and 2.20 (s). |
Performance Comparisons
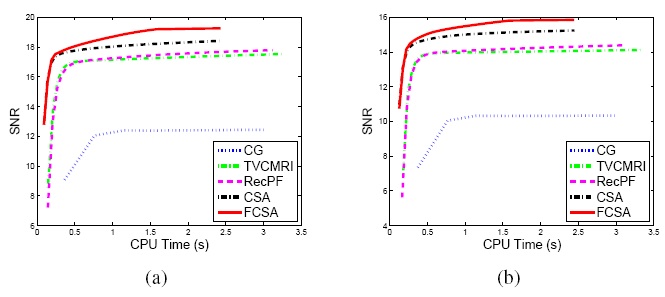 |
Figure.
Performance comparisons (CPU-Time vs. SNR) on different MR
images: a) Cardiac image and (b) Brain image. |
Related Sources
[1] SparseMRI
[2] TVMRI
[3] RecPF
Low Rank Tensor Completion
Visual Comparison
 |
Figure.
Comparisons in terms of visual effects. Color images
are: (1)Window; (2) Cherry; (3) Sheep and (4) Fish. The column
(a), (b), (c) and (d) correspond to the images before completion,
the obtained results by the CGD-LRTC, APG-LRMC and FCSA-LRTC,
respectively. |
Performance Comparisons
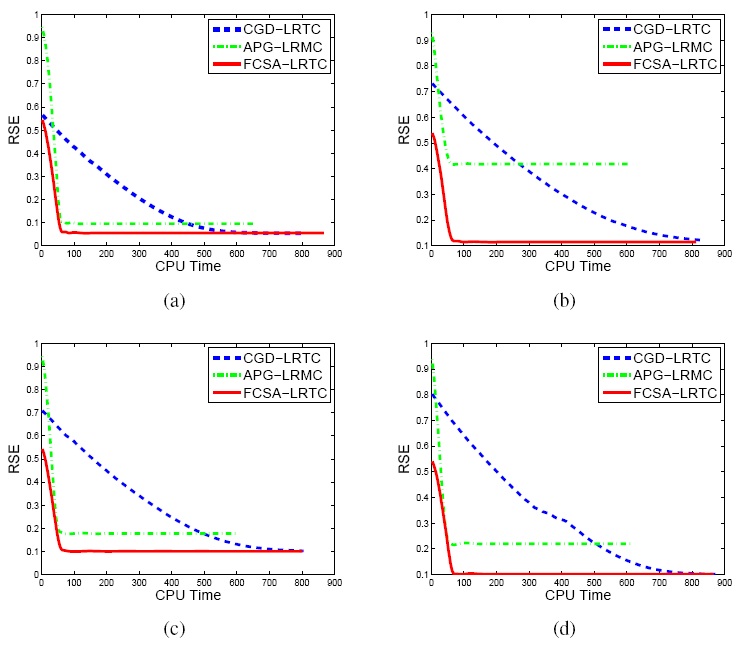 |
Figure.
Performance comparisons in terms of the CPU Time and RSE:
a)Window image; b) Cherry image; c) Sheep image and (d) Fish
image. |
Related Sources