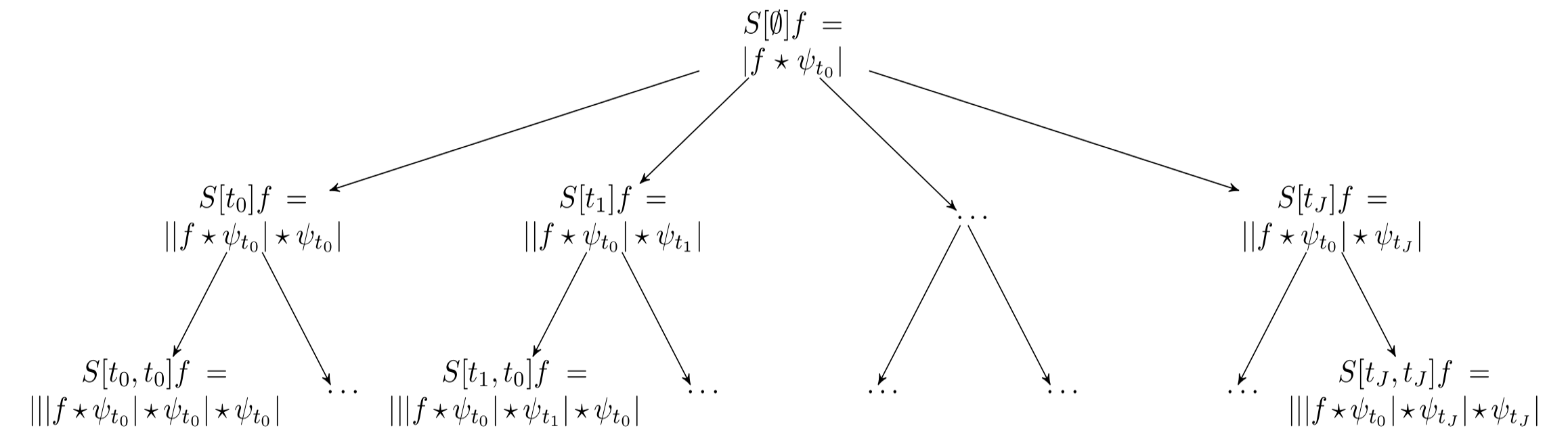
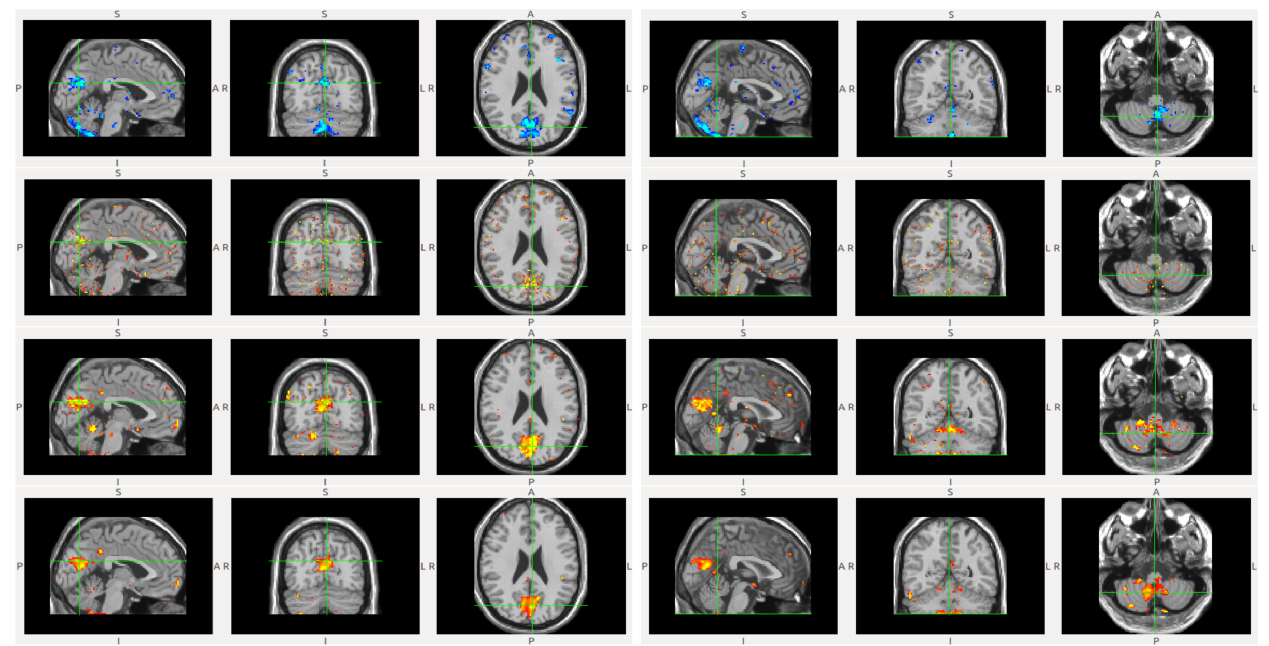
A variety of studies in neuroscience/neuroimaging seek to perform statistical inference on the acquired brain image scans for diagnosis as well as understanding the pathological manifestation of diseases. To do so, an important first step is to register (or co-register) all of the image data into a common coordinate system. This permits meaningful comparison of the intensities at each voxel across groups (e.g., diseased versus healthy) to evaluate the effects of the disease and/or use machine learning algorithms in a subsequent step. But errors in the underlying registration make this problematic, they either decrease the statistical power or make the follow-up inference tasks less effective/accurate. In this paper, we derive a novel algorithm which offers immunity to local errors in the underlying deformation field obtained from registration procedures. By deriving a deformation invariant representation of the image, the downstream analysis can be made more robust as if one had access to a (hypothetical) far superior registration procedure. Our algorithm is based on recent work on scattering transform. Using this as a starting point, we show how results from harmonic analysis (especially, non-Euclidean wavelets) yields strategies for designing deformation and additive noise invariant representations of large 3-D brain image volumes. We present a set of results on synthetic and real brain images where we achieve robust statistical analysis even in the presence of substantial deformation errors; here, standard analysis procedures significantly under-perform and fail to identify the true signal.
This research was supported by NIH R01AG040396, NIH R01AG021155, NSF CAREER Award RI1252725. Partial support was provided by UW ADRC AG033514), UW ICTR (1UL1RR025011), UW CPCP (AI117924) and NIH grants AG010129 and AG027161.