
As more 3-D surface models are available online, it becomes important to parse the shape into perceptually sementic regions,
which serve as a key role in computer animation, texture mapping, morphing, and shape retrival.
Ideally, the algorithm should ignore local noise and instead focus on topological features that are globally meaningful.
But the importance of a feature (or artifact) is invariably modulated by both its local and global context.
In order to derive analysis on shape surfaces, we define MWKD on surface models.
Wavelet Kernel Descriptor (WKD) is a multi-resolutional descriptor that captures the behavior of a wavelet function in multiple frequency levels,
and MWKD is derived based on the maximum WKD in multiple scales.
The MWKD is robust to surface noise, and consistent along deformation.
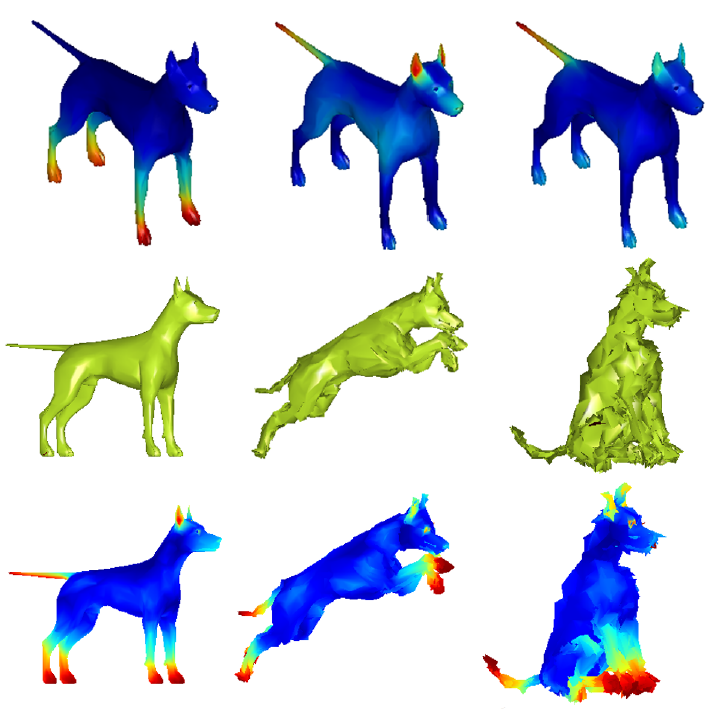
The exterimas of the MWKD is collected as the interest points (IP), and clustering other vertices around the IP forms the segmentation of the surfaces.
It usually picks the surfaces that peak out of the main body.
The segmentation result has find-to-coarse behaviors, and is robust to different poses of the shape.


This research is supported by
NIH R01AG040396,
NIH R01AG021155,
NSF RI1116584,
NSF RI1252725,
the Wisconsin Partnership Proposal, UW ADRC, and UW ICTR (1UL1RR025011).
1. D. Hammond et al, Wavelets on graphs via spectral graph theory, Applied and Computational Harmonic Analysis, 2011.
2. W. Kim et al, Multi-resolution Shape Analysis via Non-EuclideanWavelets: Applications to Mesh Segmentation and Surface Alignment Problems, CVPR, 2013.