3-D Brain Surface Registration and Alignment

Finding brain region correspndence

Alignment of a pair of 3-D surfaces is an important problem especially in brain imaging, where scientists are interested in identifying disease specific effects on measures such as cortical thickness (which can be thought of a function defined on the surface).

Registration by Wavelets in Non-Euclidean Space

Vertex to vertex correspondences can be matched by minimizing the L2 norm of wavelet coefficients from the vertex coordinates. (The proof is given in [2].)

Three different brain surfaces, and the eigenfunction of the first surface (template) is projected onto the second and the third surface by the wavelet registration.

Surface Alignment by Wavelets in Non-Euclidean Space

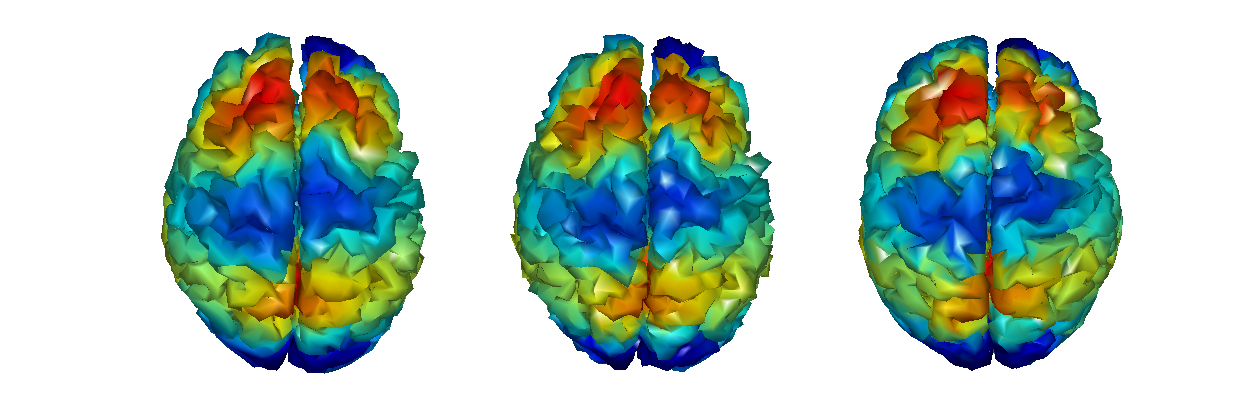
Using sampled wavelet coefficients from a brain surface by the correspondences to a template, and reconstruct using the bases from the template yields a transformed brain surface with the same topology of the template.

The second and the third surface is aligned to the first surface (template) by wavelet coefficients from the registration and the bases from the template surface. As a result, all three surfaces now have the same topology. The 20th eigenfunctions from each surface are plotted, which are now the same.

Acknowledgment

This research is supported by NIH R01AG040396, NIH R01AG021155, NSF RI1116584, NSF RI1252725, the Wisconsin Partnership Proposal, UW ADRC, and UW ICTR (1UL1RR025011).

 

Reference

1. D. Hammond et al, Wavelets on graphs via spectral graph theory, Applied and Computational Harmonic Analysis, 2011.
2. W. Kim et al, Multi-resolution Shape Analysis via Non-EuclideanWavelets: Applications to Mesh Segmentation and Surface Alignment Problems, CVPR, 2013.