Latent Variable Graphical Model Selection using Harmonic Analysis

Abstract

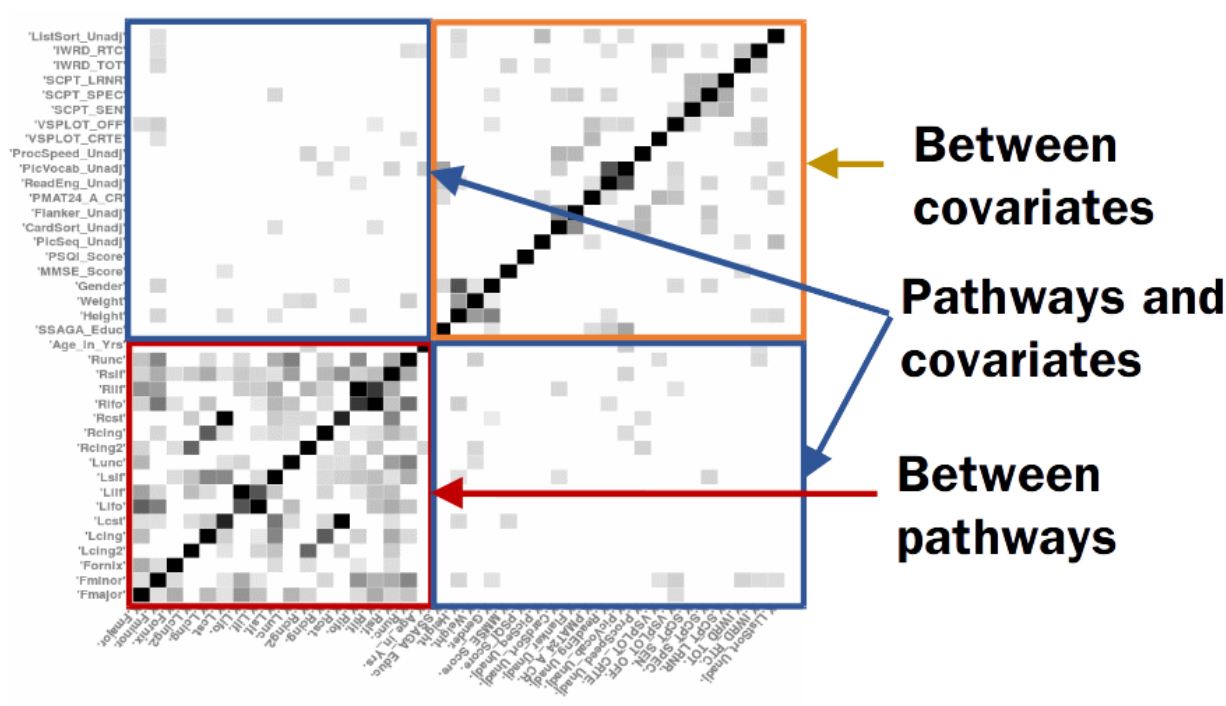
A major goal of imaging studies such as the (ongoing) Human Connectome Project (HCP) is to characterize the structural network map of the human brain and identify its associations with covariates such as genotype, risk factors, and so on that correspond to an individual. But the set of image derived measures and the set of covariates are both large, so we must first estimate a ‘parsimonious’ set of relations between the measurements. For instance, a Gaussian graphical model will show conditional independences between the random variables, which can then be used to setup specific downstream analyses. But most such data involve a large list of ‘latent’ variables that remain unobserved, yet affect the ‘observed’ variables sustantially. Ac- counting for such latent variables is not directly addressed by standard precision matrix estimation, and is tackled via highly specialized optimization methods. This paper offers a unique harmonic analysis view of this problem. By casting the estimation of the precision matrix in terms of a composition of low-frequency latent variables and high-frequency sparse terms, we show how the problem can be formulated using a new wavelet-type expansion in non-Euclidean spaces. Our formulation poses the estimation problem in the frequency space and shows how it can be solved by a simple sub-gradient scheme. We provide a set of scientific results on ∼500 scans from the recently released HCP data where our algorithm recovers highly interpretable and sparse conditional dependencies between brain connectivity pathways and well-known covariates.

Fig. Left: effect of latent variables causing dense precision matrix, Right: removing the effect of latent varibles returning sparse precision matrix.

Experimental Results on Human Connectome Project (HCP)

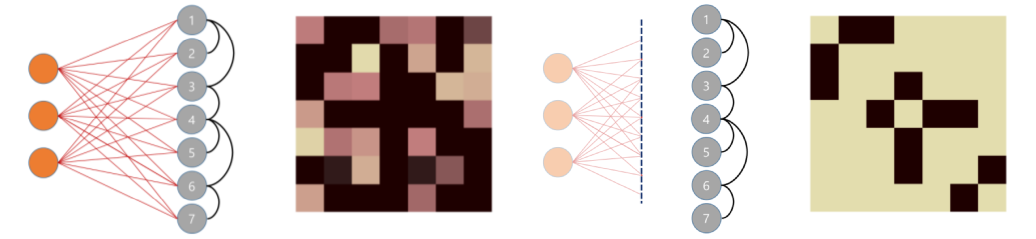
The objective of the experiment is to recover a sparse (and interpretable) precision matrix explaining the conditional dependencies among the variables despite latent variables.

Imaging Data: tractography (structural brain connectivity) derived from Diffusion Tensor Image (DTI) from HCP over 489 participants and 17 major white-matter connectivities selected.

Non-imaging Data: 22 non-imaging covariates (out of ∼350) related to demographics, physical health, memory, sleep and etc.

Fig. Estimated precision matrix on HCP dataset.

Acknowledgment

This research was supported by NIH R01AG040396, NSF CAREER Award RI1252725, UW ADRC AG033514, UW ICTR 1UL1RR025011, UW CPCP AI117924 and Waisman Core Grant P30 HD003352-45.

Reference

1. Won Hwa Kim*, Hyunwoo J. Kim*, Nagesh Adluru, Vikas Singh, "Latent Variable Graphical Model Selection using Harmonic Analysis: Applications to the Human Connectome Project (HCP)", Computer Vision and Pattern Recognition (CVPR), 2016.